[파이썬][데이터분석] 데이터 분석과 머신러닝 - Basic Derivative

1.4 Basic Derivation

미분

우리가 수학시간에 많이 들어봤던 단어로 말 그대로 작게 나누는 것이다. X라는 값이 들어갔을 때 해당 값을 나누는 것이다.

미분을 파이썬으로 구현하는 방법은 대표적으로 2가지가 있다.

• 직접 구현하는 경우

  def numerical_diff(f, x):
    delta = 0.001 # 매우 작은 값
  
    return (f(x+delta) - f(x)) / delta
  

• Scipy 라이브러리를 이용한 경우 ```python from scipy.misc import derivative

## 편미분

다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 간주하고 미분하는 방법이다.
머신러닝에서는 파라미터가 2개 이상인 Error 함수에서 우선 1개의 파라미터에 대해 미분하는 방법으로 사용된다.

sympy 라이브러리를 통해 구현이 가능하다.

```python
import sympy as sym
from sympy.abc import x, y, e

sym.diff(함수, 원하는 미분만큼의 변수)

Chain Rule

함수의 함수를 미분하는 방법으로 합성함수라고 부르기도 한다. 마치 양파를 깔 때 바깥면에서부터 껍질을 까야하는 것처럼 Chain Rule 역시 미분을 할 때 바깥 함수부터 미분하여 안의 함수를 미분한다.

머신러닝에서의 실사용

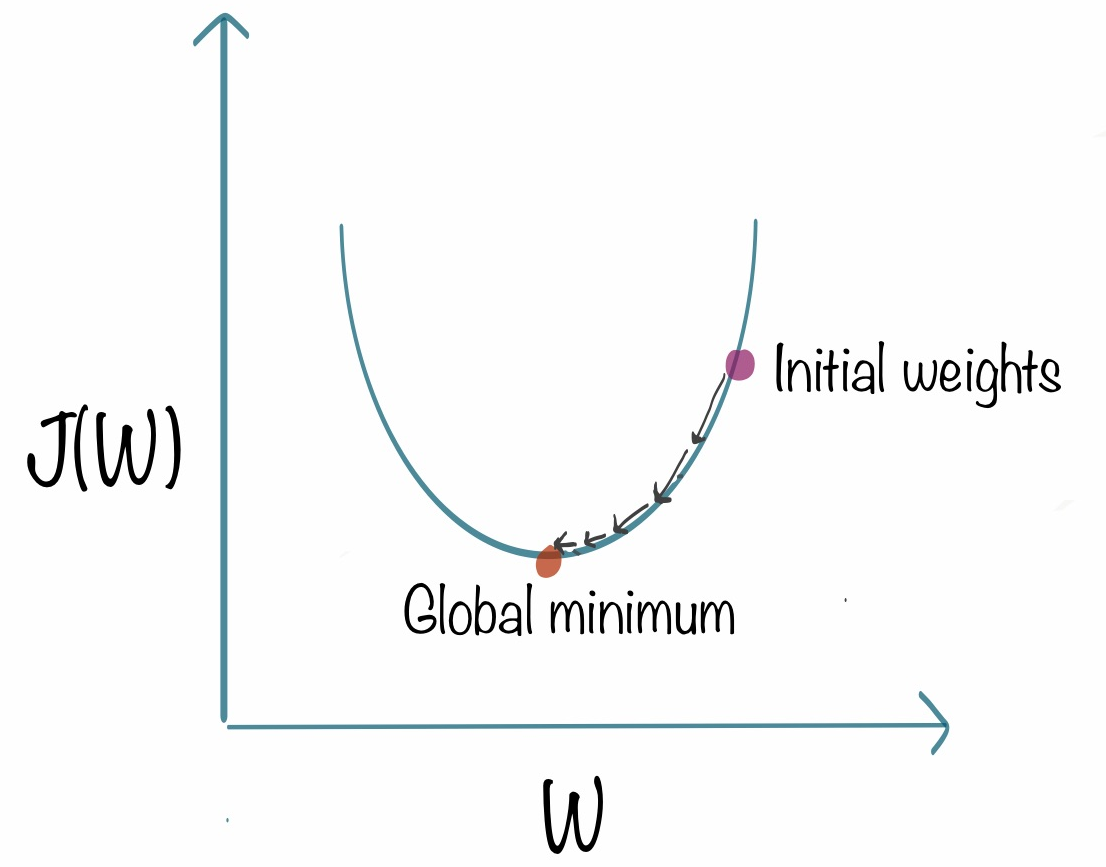
경사 하강법

• Gradient Descent, 경사하강법은 오차 함수인 e을 최소화하는 a, b값을 찾을 수 있는 최적화 알고리즘중 하나이다.

사진 출처 : Kdbuggets

• 파이썬으로 구현 ```python def gradient_descent(X, y, lr = 0.05, epoch = 10):

  a, b = 0.21, 0.49 # 임의의 파라미터를 넣는다. N = len(X)

  for _ in range(epoch):
  f = y - (a*X + b)

    # a와 b를 업데이트
    a -= lr * (-2 * X.dot(f).sum() / N)
    b -= lr * (-2 * f.sum() / N)        
  

```

위의 epoch는 돌아가는 횟수를 말하는데 해당 수를 변경하여 경사하강을 몇 번 진행할 것인지 정하면 된다.